Presentación

Veremos ahora un problema un poco menos directo que los anteriores. Se trata de un problema que puede ser resuelto mediante un algoritmo que puede considerarse de programación dinámica. Vamos concretamente a estudiar el problema 108 del juez on-line de la UVA:

PROBLEMA 108. Maximum Sum: Enunciado del problema en el juez on-line de la UVA

El enunciado es simple: dada una matriz cuadrada de números enteros de tamaño N × N, encontrar el máximo de los valores que sean suma de los elementos de cualquier submatriz de tamaño M × P, con 1 ≤ M, P ≤ N que se puedan definir dentro de la matriz original. Nótese que en general la submatriz no tiene que ser cuadrada.

¡CUIDADO! El enunciado de este problema en el juez on-line está mal. Habla de un único caso de entrada, cuando en realidad puede haber más de uno. El final de la entrada se detecta por el final o por un valor de N = 0.

Si el alumno se siente capaz, puede intentar resolver el problema sin seguir leyendo más adelante el análisis que sigue a continuación.

Continuar con la lectura del análisis del problema y su enunciado.

Análisis del problema y su enunciado

Como dijimos antes, este es un problema que puede ser resuelto mediante un algoritmo que "puede considerarse" de programación dinámica. La razón por la que empleamos esta expresión es porque si bien el algoritmo emplea técnicas de programación dinámica, en el sentido de que almacena resultados ya calculados para no repetir varias veces esos mismos cálculos, no es menos cierto que son necesarios cálculos y tratamientos adicionales diseñados ad-hoc para este caso concreto.

El algoritmo elemental de fuerza bruta consistiría en los siguientes tratamientos:

1. Enumerar todos los posibles extremos superior-izquierdos de la submatriz. Esto sería un tratamiento en Θ(N²).
2. Para cada extremo superior-izquierdo, enumerar todos los posibles extremos inferior-derechos que se pueden tomar para definir la submatriz. Este tratamiento estaría también en Θ(N²).
3. Sumar todos los elementos de la submatriz definida y tomar el máximo de todos esos valores. Este tratamiento estará en el orden del número de elementos de la submatriz, que en general estará en Θ(N²).

Como puede observarse, este es un algoritmo altamente ineficiente. Su tiempo de ejecución está en Θ(N⁶). El siguiente programa Pascal implementa este algoritmo y, como cabe esperar, es rechazado por el juez on-line por exceder el límite de tiempo de ejecución:

Programa Pascal algoritmo de fuerza bruta

program p108fuerzabruta;

const
    MAX_N = 100;

type
    Tipo_Rango  = 1 .. MAX_N;
    Tipo_Matriz = array [Tipo_Rango, Tipo_Rango] of Integer;

var
    A : Tipo_Matriz;

    i, j, i_si, j_si, i_id, j_id : Tipo_Rango;
    suma, mayor : Longint;
    N : Integer;

begin
    repeat

    N := 0;
    read (N);

    if N = 0 then break;

    for i := 1 to N do
        for j := 1 to N do
            read (A[i,j]);

    mayor := A[1,1];

    for i_si := 1 to N do (* i del extremo superior-izquierdo *)
        for j_si := 1 to N do (* j del extremo superior-izquierdo *)
            for i_id := i_si to N do (* i del extremo inferior-derecho *)
                for j_id := j_si to N do (* j del extremo inferior-derecho *)
                begin
                    suma := 0;
                    for i := i_si to i_id do
                        for j := j_si to j_id do
                            suma := suma + A[i,j];
                    if suma > mayor then mayor := suma
                end;

    writeln (mayor)
    until False
end.

Es fácil comprobar que hay muchos cálculos que se repiten en este programa. Una misma submatriz se suma una y otra vez en cada submatriz mayor que la contiene. Es posible almacenar algunos de estos cálculos e incluso precalcular ciertos otros para no repetirlos tanto.

¿Sabes de qué forma?

Continuar leyendo pistas de resolución del ejercicio.

Primera pista:

Hay un tratamiento que en cierto modo podría considerarse preprocesamiento y que puede irse realizando conforme se van tomando los datos de la entrada. Se trata de hacer que cada elemento de una columna (o fila) almacene la suma acumulativa de todos los elementos de la columna/fila hasta él inclusive.

Si por ejemplo lo hiciésemos por filas, si llamamos t a la tabla de datos de entrada y a a la tabla que vamos a manejar en el programa, el elemento a_i,j de esta tabla podría definirse como:

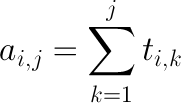
De este modo, dada una cierta fila k podríamos calcular la suma de los elementos de la fila k desde la columna j hasta la i (donde j ≤ i) en O(1) sencillamente como a_k,i – a_k,j –1.

El único problema que plantea lo anterior es el valor de j = 1, que provocaría acceder a la columna 0, que caería fuera de los límites de la tabla. Una posible solución es incluir el cero en el conjunto de índices de las columnas (inevitable, por otra parte, en el lenguaje C) y establecer todos los valores de esa columna como 0. De este modo es válido el análisis realizado antes.

De este modo, utilizando este preprocesamiento y partiendo de unas definiciones como las siguientes:

Código C/C++: declaraciones de la tabla que maneja los datos de este problema:

#define MAX_N   100

typedef long int Tipo_Matriz[MAX_N+1][MAX_N+1];

Tipo_Matriz a;

int N; // tamaño del caso de entrada (no superará a MAX_N)

, suponiendo que el valor de n ya ha sido leído, los datos de entrada podrían tomarse y preprocesarse del siguiente modo:

Código C++: entrada de datos y preprocesamiento:

    for (i = 1; i <= N; i++)
        for (j = 1; j <= N; j++) {
            long int valor;
            cin >> valor;
            a[i][j] = a[i][j-1] + valor;
        }

Como puede observarse, este tratamiento se realiza en el mismo tiempo (asintótico) que se leen los datos de la entrada, por lo que se puede decir que antes de empezar ya hemos hecho algunos cálculos. Con los datos dispuestos de esta forma, y con la consideración que hicimos sobre cómo calcular en O(1) la suma de cualquier segmento de una fila, la complejidad de la solución se puede reducir drásticamente. ¿Sabes cómo?

Continuar leyendo la siguiente pista para de resolución del ejercicio.

Segunda pista:

Dado un par cualquiera de columnas j e i, donde j ≤ i, es posible calcular el valor máximo de la suma de los elementos para cada una de las submatrices acotadas entre estas dos columnas en un tiempo que está en Θ(N).

Para ello es preciso hacer uso de que la suma de los elementos de una fila entre esas dos columnas se puede calcular en O(1), tal como explicamos antes, y el algoritmo de Kadane de cálculo de la subsecuencia de mayor peso.

En este momento el lector tiene toda la información necesaria para diseñar un algoritmo que resuelve el problema en un tiempo que está en Θ(N³), lo cual es sustancialmente mejor que el Θ(N⁶) del algoritmo de fuerza bruta que vimos anteriormente.

Ver el listado del programa que resuelve el problema.

Listado del programa:

Programa C++:

#include <iostream>
using namespace std;

#define MAX_N   100

typedef long int Tipo_Matriz[MAX_N+1][MAX_N+1];

Tipo_Matriz a;


int main (void)
{
    int N, i, j, k;
    long int sig, mt_c, max_ab, max_sum;

    for (i = 1; i <= MAX_N; i++)
        a[i][0] = 0;

    while ((cin >> N) && N) {
 
        for (i = 1; i <= N; i++)
            for (j = 1; j <= N; j++) {
                long int valor;
                cin >> valor;
                a[i][j] = a[i][j-1] + valor;
            }

        max_sum = a[1][1];
        for (j = 1; j <= N; j++)
            for (i = j; i <= N; i++) {
                mt_c = a[1][i] - a[1][j-1];
                for (k = 2; k <= N; k++) {
                    sig = a[k][i] - a[k][j-1];
                    if (mt_c + sig > sig)
                        mt_c = mt_c + sig;
                    else
                        mt_c = sig;
                    if (mt_c > max_sum)
                        max_sum = mt_c;
                }
            }

        cout << max_sum << endl;
    }
    return 0;
}

Olimpiada de programación - Facultad de Informática - Universidad de Murcia