CURSO ON-LINE DE PREPARACIÓN

 

Sesión 5. Más problemas de grafos.

Introducción y generalidades

Recordad que hay tres tareas principales en este curso: practicar, practicar y practicar, resolviendo cuantos más problemas mejor. Debes concienciarte de que la mejor y única forma de mejorar tus habilidades de resolución de problemas es... resolviendo problemas.

Con el fin de ofrecer más herramientas de práctica, en esta sesión vamos a presentar un nuevo juez on-line: el de la Olimpiada Informática Española. Dentro de este juez vamos a discutir un problema de grafos de complejidad media-alta, planteando diversas soluciones.

El juez de la Olimpiada Informática Española (OIE)

La OIE es un concurso de programación dirigido a todos los alumnos de bachillerato y secundaria de España. Dicho así, podría parecer que este concurso tiene un nivel insuficiente para nuestros propósitos. Sin embargo, debemos aclarar que el nivel de los problemas más complejos no tiene nada que envidiar a muchos de los problemas típicos de las olimpiadas universitarias. Así que, teniendo este recurso, ¿por qué desaprovecharlo?

Para acceder a los problemas del juez de la OIE es necesario registrarse en:

De forma periódica se organizan concursos on-line de preparación, en los que van apareciendo problemas nuevos. Los problemas están clasificados en diferentes categorías: introductorios, simulación, voraces, numéricos, etc. La colección de programación dinámica es especialmente completa e interesante. Merece la pena echar un vistazo a todas las categorías.

Una característica específica de la OIE (y también de la Olimpida Internacional Informática (IOI)), en relación a los concursos universitarios, es el hecho de que en cada problema podemos obtener entre 0 y 100 puntos. Los problemas tienen diferentes casos de prueba, en orden creciente de dificultad. Cuantos más casos de prueba pueda resolver nuestro programa, es decir, cuanto mejor sea nuestra solución, más puntos podemos obtener de ese problema.

Normalmente esta dificultad de los problemas está relacionada con el tamaño de los casos de prueba. Por ejemplo, en un problema de grafos hipotético, podríamos obtener hasta 40 puntos si resolvemos el problema con grafos de 10 nodos; 80 puntos si lo resolvemos con grafos de 1000 nodos; y 100 puntos si lo resolvemos con grafos de 10000 nodos. El tipo de algoritmos que pueden servir para resolver el problema para 10 nodos, puede ser completamente ineficiente para 1000 nodos o más.

Problema de ejemplo

Una vez presentado el juez de la OIE, vamos a trabajar con un problema del mismo. Se trata de un problema de grafos, que apareció en el quinto concurso on-line de preparación:

PROBLEMA: Warp-world : Enunciado del problema - Enlace al juez (recuerda registrarte en este juez)

Se trata de una nueva variante de los problemas de tableros y laberintos. Tenemos un tablero que representa un mapa de posiciones. El objetivo es encontrar el camino más corto entre dos posiciones (la "(1)" y la "(2)"). Podemos movernos arriba, abajo, a la izquierda o a la derecha. La particularidad es que algunas casillas (las que tienen las mismas letras) son equivalentes entre sí, por lo que podemos movernos a cualquiera de ellas de manera instantátena.

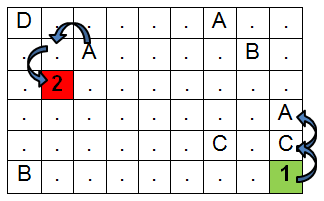
Ejemplo: Un tablero del problema y un recorrido sobre el mismo. Los warps-points (las casillas que tienen letras) son posiciones equivalentes entre sí; podemos movernos instantáneamente entre los que tienen la misma letra. También podemos pasar por encima de ellos sin cambiar de posición. En este ejemplo, la distancia mínima entre (1) y (2) es de 4.

Un método sencillo para resolverlo

Se puede ver muy fácilmente que se trata de un problema de caminos mínimos. Los nodos del grafo son cada una de las casillas del tablero; las aristas son las cuatro posiciones adyacentes a cada casilla, más las aristas correspondientes a los warp-points (que serían aristas de coste 0 entre todos los warps-points con la misma letra).

Una vez construido el grafo, podemos calcular el camino mínimo entre (1) y (2) usando el algoritmo de Dijkstra. Equivalentemente, recordemos que cuando las aristas de un grafo son de coste 1, se pueden calcular los caminos mínimos usando la búsqueda primero en anchura partiendo del nodo origen. Por lo tanto, un algoritmo sencillo para obtener la solución del problema podría ser el siguiente. En adelante, suponemos que la posición (1) es (x1, y1), y la posición 2 es (x2, y2):

1. Crear una matriz D, del mismo tamaño que el tablero, para calcular los costes de los caminos. Inicializarla a INFINITO (un valor muy grande), para indicar que todavía no hemos calculado la solución.

2. Crear una cola de posiciones, C (es decir, una cola donde cada elemento es un par (x, y)), metiendo inicialmente (x1, y1) en la cola.  Inicializar también D[x1, y1] a valor 0.

3. Repetir:
   3.1. Sacar el tope de la cola. Supongamos que es (x, y).
   3.2. Si el tope es igual a (x2, y2), entonces acabamos. Ya sabemos su coste mínimo en D[x2, y2].
   3.3. En otro caso, para cada una de las cuatro casillas adyacentes, (xa, ya), de (x, y) hacer:
      3.3.1. Si D[x, y]+1 es menor que D[xa, ya] entonces:
         3.3.1.1. Actualizar D[xa, ya] con D[x1, y1]+1. Meter en la cola (xa, ya).
         3.3.1.2. Si (xa, ya) es un wrap-point, actualizar todas las casillas equivalentes (xe, ye) (es decir, las que tengan la misma letra que (xa, ya)) con el mismo valor que D[xa, ya] y meterlas también todas en la cola. Para optimizar este paso, podemos tener almacenado en un array de 26 posiciones, para cada letra, todas las casillas que tengan esa letra.

Observar que estamos haciendo un algoritmo de búsqueda primero en anchura sobre un grafo, aunque sin construir explícitamente el grafo (en el peor caso, con 400 filas y columnas, el número de nodos del grafo sería de 160.000).

Estudio de complejidad del método

El anterior algoritmo es capaz de resolver el problema planteado. Pero, ¿será suficientemente rápido? La eficiencia de la búsqueda primero en anchura, sin construir explícitamente el grafo, sería de O(n+a), siendo n el número de nodos y a el número de aristas. Como en este problema a se puede considerar proporcional a n, podemos decir que el tiempo es un O(n) para cada consulta.

En el problema se nos pide resolver k preguntas por cada tablero, por lo que el tiempo total sería de O(k*n). ¿Es eso suficientemente rápido?

En el segundo caso (100 filas y columnas y 100 preguntas), sería proporcional a: 100*100*100 = 1.000.000. No hay problema.

Pasemos al tercer caso (200 filas y columnas y 1.000 preguntas), tenemos: 200*200*1000 = 40.000.000. Vaya, ya está un poco más justo...

En el cuarto caso (400 filas y columnas y 10.000 preguntas), tenemos: 1.600.000.000. ¡Imposible!

En búsqueda de una solución más eficiente

No nos queda más remedio que buscar un método más eficiente para resolver el problema. Con casos que contienen 10.000 preguntas (es decir, calcular 10.000 caminos mínimos) parece deducirse que necesitamos algún método capaz de resolver cada consulta en un tiempo constante.

Vamos a partir de la siguiente idea: todos los warp-points con la misma letra pueden considerarse realmente como un solo nodo. Por lo tanto, tenemos los 26 posibles nodos de los  warp-points (uno por cada letra), más las posiciones sin letras. El camino mínimo de (1) a (2) puede pasar por los warp-points o no; así que debemos calcular caminos mínimos entre los warp-points.

El algoritmo sería como el siguiente:

1. Para cada tipo de warp-points, desde la A a la Z, calcular una matriz del tamaño del tablero, donde en cada casilla se calcule la distancia mínima de esa casilla a cualquiera de ese tipo de warp-point. Esto puede hacerse de manera eficiente con una búsqueda primero en anchura, como la descrita en el punto anterior, inicializando todas las posiciones de esa letra a 0. Vamos a llamar a estas matrices TAB[i], siendo i= A, B, ..., Z; de manera que TAB[i][x, y] indica el coste del camino mínimo de (x, y) a un warp-point de tipo i.
2. Para cada par de letras (i, j), calcular la distancia mínima de ir directamente desde un warp-point de tipo i hasta otro de tipo j, sin pasar por otros warp-point. Sea C[i, j] esa matriz. Se puede hacer de forma eficiente usando TAB[i], buscando en esa matriz el mínimo de las posiciones donde haya un warp-point de tipo j en el tablero.
3. Aplicar Floyd sobre C, obteniendo una matriz D, donde cada D[i, j] guardará el camino mínimo de cualquier warp-point de tipo i a cualquier warp-point de tipo j.
4. Ahora, cada consulta se puede hacer en un O(26*26). El camino mínimo de (1) a (2) puede ser de varios tipos:
1. Sin pasar por ningún warp-point: se puede calcular de forma trivial con la distancia de Manhattan de (1) a (2), es decir: abs(x1-x2) + abs(y1-y2).
2. Pasando por un solo warp-point: buscar el mínimo, para cada i= A, B, ..., Z, de la suma: TAB[i][x1, y1] + TAB[i][x2, y2].
3. Pasando por dos o más warp-points: realmente lo único que nos interesa son el warp-point de entrada y el de salida. Así que debemos buscar el mínimo, para cada i y para cada j, de la suma: TAB[i][x1, y1] + D[i, j] + TAB[j][x2, y2].
   

Obviamente, hemos complicado un poco la resolución del problema. Pero, en cambio, hemos conseguido un método más eficiente, puesto que se precalculan muchos costes de caminos mínimos.

Estudio de complejidad del método optimizado

¿Será suficientemente rápido el nuevo método? Vamos a analizar cada uno de los pasos anteriores:

1. En este paso, cada matriz TAB[i] se puede calcular con una búsqueda primero en anchura, que ya hemos visto que es un O(n). Por lo tanto, el tiempo total de este paso sería de O(26n).
2. En este segundo paso, para cada matriz TAB[i], deberíamos recorrer todas sus posiciones. Como hay 26 de estas matrices, el tiempo sería de O(26n).
3. Aplicamos un algoritmo de Floyd sobre un grafo de tamaño 26, por lo que el orden de complejidad sería O(26*26*26).
4. Debemos buscar el mínimo entre tres posibles opciones. La primera de ellas se puede calcular en un O(1), la segunda en un O(26), y la tercera en un O(26*26). Como tenemos k consultas, tenemos O(26*26*k).

Por lo tanto, el orden de complejidad total sería: O(2*26n + 26*26*k). Considerando el caso más grande (400 filas y columnas y 10.000 preguntas), tenemos que el número de operaciones sería proporcional a: 2*26*400*400 + 26*26*10.000 = 8.320.000 + 6.760.000 = 15.080.000 operaciones. Lo cual es más de 100 veces más rápido que el método sencillo. Con una implementación suficientemente cuidada, el algoritmo entraría perfectamente en tiempo. Como ejercicio, dejamos a los alumnos la implementación de este método.

Problemas propuestos

El número de problemas interesantes que podemos encontrar en el juez on-line de la OIE es muy grande. En esta sesión no vamos a proponer un problema concreto, sino que dejamos a elección entre todos los problemas de grafos del juez de la OIE. Recordamos que los problemas están clasificados con medallas de bronce, plata, oro y copa, en nivel creciente de dificultad. Como ya dijimos, para que los enlaces funcionen es necesario registrarse en dicho juez. 

		Harrichu y el laberinto (OIE08/p1)	4harrichu
		The Voight-Kampff test	voightkampff
		Velocirráptors 101 (OIE08/F1)	velo101
		Papa Noel y su trineo (OIE09/p3)	trineo-noel
		Los regalos de Papa Noel (2) (OIE09/p3)	regalos-noel2
		Amigos (OIE09/c2)	amigos
		Tratado de paz 2 (OIE09/p11)	tratado-paz2
		Harrichu y la competición ciclista (OIE09/p13)	harrichuciclista
		El de Indiana Jones (OIE08/F2)	indiana
		Más amigos (OIE10/p9)	masamigos
		El burro de ajedrez (OIE10/p13)	donkey-chess
		Derrame de petróleo (OIE10/p13)	oil-spill-1
		Derrame de petróleo (2) (OIE10/p13)	oil-spill-2

Olimpiada de programación- Facultad de Informática - Universidad de Murcia